Triedro de Frenet

O triedro de Frenet foi criado por Jean Frédéric Frenet (Périgueux, 7 de fevereiro de 1816 — Périgueux, 12 de junho de 1900) professor, astrônomo, matemático e meteorologista francês.

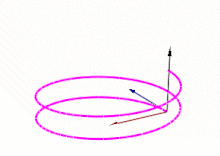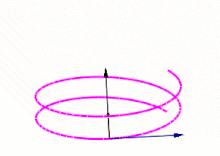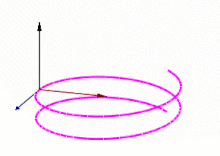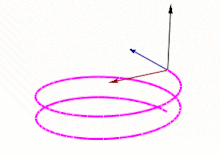
É um conjunto abstrato de três vetores^[1] (T, N e B) que diz respeito a propriedades cinemáticas de uma partícula que se move em uma trajetória curvilínea, usado em cálculo vetorial. No triedro, o vetor T representa a tangente à curva, o vetor N é a derivada de T, e o vetor B é o produto vetorial de T e N.

Em resumo, as formulas do triedro de Frenet-Serret são:

${\displaystyle {d{\vec {\mathrm {T} }} \over ds}=\kappa {\vec {\mathrm {N} }},{d{\vec {\mathrm {N} }} \over ds}=-\kappa {\vec {\mathrm {T} }}+\tau {\vec {\mathrm {B} }},{d{\vec {\mathrm {B} }} \over ds}=-\tau {\vec {\mathrm {N} }},}$

Onde d/ds é o derivativo com respeito ao comprimento de arco, κ é a curvatura e τ é a torção da curva. Os esclares κ e τ definem efetivamente a curvatura e a torção em uma curva no espaço. Intuitivamente, curvatura mede a falha de uma curva em ser uma linha reta, enquanto a torção mede a falha de uma curva em ser planar.

Aplicações

Em cálculo .vetorial, as fórmulas de Frenet–Serret descrevem as propriedades cinemáticas de uma partícula que se move ao longo de uma curva contínua e diferenciável, num espaço euclidiano tridimensional R³, ou as propriedades geométricas da própria curva independentemente do movimento. Mais especificamente, as fórmulas descrevem as derivadas dos vetores unitários tangente, normal, e binormal uns em relação aos outros. Diferentemente dos vetores unitários ${\displaystyle {\vec {i}},{\vec {j}}}$ e ${\displaystyle {\vec {k}}}$ , os vetores ${\displaystyle {\vec {T}},{\vec {N}}}$ e ${\displaystyle {\vec {B}}}$ acompanham toda a trajetória através da curva.

As fórmulas de Jean Frédéric Frenet foram apresentadas na sua tese de 1847, e por Joseph Alfred Serret em 1851. A notação dos vetores e de álgebra linear usada hoje para estas fórmulas não estava ainda em uso aquando da sua exposição por estes matemáticos.

Os vetores unitários tangente, normal, e binormal, designados por ${\displaystyle {\vec {T}},{\vec {N}}}$ e ${\displaystyle {\vec {B}}}$, ou triedro de Frenet–Serret, são definidos por:

• ${\displaystyle {\vec {T}}}$ é o vetor unitário e tangente à curva, e aponta na direção do movimento.
• ${\displaystyle {\vec {N}}}$ é a derivada de ${\displaystyle {\vec {T}}}$ em relação ao arco-comprimento, dividida pela curvatura.
• ${\displaystyle {\vec {B}}}$ é o produto vetorial de ${\displaystyle {\vec {T}}}$ e ${\displaystyle {\vec {N}}}$.

Definições

Seja C uma curva representada por ${\displaystyle {\vec {r}}(t)=x(t){\vec {i}}+y(t){\vec {j}}+z(t){\vec {k}}}$ no espaço euclidiano, representando o vetor posição da partícula em função do tempo. As fórmulas de Frenet-Serret aplicam-se a curvas não degeneradas, o que significa que elas têm curvatura diferente de zero. Mais formalmente, nesta situação, o vetor de velocidade ${\displaystyle {\vec {r}}}$'(t) e o vetor de aceleração ${\displaystyle {\vec {r}}}$''(t) são necessariamente não-proporcionais.

Com s(t) representando o comprimento de arco que a partícula moveu ao longo da curva no tempo t. A quantidade s é usada para dar a curva traçada pela trajetória da partícula uma parametrização natural pelo comprimento do arco, uma vez que muitos caminhos diferentes de partículas podem traçar a mesma curva geométrica percorrendo-a em diferentes taxas. Em detalhe, s é dado por

${\displaystyle s(t)=\int _{0}^{t}\lVert r'(\sigma )\rVert d\sigma }$

Além disso, como assumimos que ${\displaystyle {\vec {r}}}$′ ${\textstyle \neq }$ 0, segue que s(t) é uma função estritamente monotonicamente crescente. Portanto, é possível resolver t como uma função de s e, assim, escrever ${\displaystyle {\vec {r}}}$(s) = ${\displaystyle {\vec {r}}}$(t(s)). A curva é assim parametrizada de uma maneira preferida: pelo seu comprimento de arco.

Com uma curva não-degenerada r(s), parametrizada pelo seu comprimento de arco, é possível, então, definir o Triedro de Frenet–Serret (ou triedro TNB):

Vetor Tangente

O vetor tangente unitário ${\displaystyle {\vec {T}}(t)}$ é definido como o vetor com a mesma direção do vetor tangente ${\displaystyle {\vec {r}}\,'(t)}$ e módulo 1.^[2]

${\displaystyle {\vec {T}}(t)={\frac {dr \over ds}{\lVert {dr \over ds}\rVert }}={\frac {{\vec {r}}(t)\,'}{|{\vec {r}}(t)\,'|}}}$

Vetor Normal

Este vetor será definido a partir da condição de ortogonalidade entre ${\displaystyle {\vec {T}}}$ e ${\displaystyle {\vec {N}}}$, ou seja, ${\displaystyle {\vec {T}}(t)\cdot {\vec {N}}(t)=0.}$ Assim, para que se comprove a definição proposta, se estabelece o seguinte teorema que embasa a demonstração.

Teorema

Se o vetor ${\displaystyle {\vec {T}}(t)}$ é um vetor de módulo constante e igual a 1, então ${\displaystyle {\vec {T}}(t)\cdot {\vec {T}}(t)\,'=0}$ e, portanto, ${\displaystyle {\vec {T}}(t)\,'}$ é ortogonal a ${\displaystyle {\vec {T}}(t)}$.

Demonstração

Considerando ${\displaystyle \mid {\overrightarrow {T}}(t)\mid }$ como constante, conforme o proposto, tem-se como o resultado do produto escalar entre as funções vetoriais ${\displaystyle {\overrightarrow {T}}(t)\cdot {\overrightarrow {T}}(t)}$ uma constante. Desta forma, fazendo-se o uso do método de derivação de um produto escalar, a Regra da cadeia, obtem-se a equação:

${\displaystyle {\begin{aligned}{\overrightarrow {T'}}(t)\cdot {\overrightarrow {T}}(t)+{\overrightarrow {T}}\cdot {\overrightarrow {T'}}(t)=0\\2{\overrightarrow {T}}(t)\cdot {\overrightarrow {T'}}(t)=0\end{aligned}}}$

Por conseguinte, é notável a veracidade da ortogonalidade dos vetores ${\displaystyle {\overrightarrow {T'}}(t)}$ e ${\displaystyle {\overrightarrow {T}}(t)}$. Então, o vetor normal fica definido como:

${\displaystyle {\vec {N}}(t)={\frac {d{\vec {T}} \over ds}{\lVert {d{\vec {T}} \over ds}\rVert }}={\frac {{\vec {T}}(t)\,'}{|{\vec {T}}(t)\,'|}}}$

O vetor normal unitário possui a mesma direção de ${\displaystyle {\vec {T}}(t)\,'}$ e aponta para o interior da curva, ou seja, para o lado côncavo de C, sendo ortogonal não só ao tangente mas também ao vetor binormal apresentado a seguir.

Vetor Binormal

O vetor binormal é um vetor unitário perpendicular a ${\displaystyle {\vec {T}}(t)}$ e ${\displaystyle {\vec {N}}(t)}$, logo

${\displaystyle {\vec {B}}(t)={\vec {T}}(t)\times {\vec {N}}(t)}$^[3]

O vetor binormal pode ser expresso, de maneira alternativa, pela seguinte equação

${\displaystyle {\vec {B}}={\frac {{\vec {r}}'(t)\times {\vec {r}}''(t)}{\lVert {\vec {r}}'(t)\times {\vec {r}}''(t)\rVert }}}$^[3]

Além disso, forma, juntamente com ${\displaystyle {\vec {T}}}$ e ${\displaystyle {\vec {N}}}$, um sistema dextrogiro.^[4]

Fórmulas de Frenet-Serret

${\displaystyle {d{\vec {T}} \over ds}=\quad \qquad \quad \kappa {\vec {N}}}$

${\displaystyle {d{\vec {N}} \over ds}=\ -\kappa {\vec {T}}\quad \qquad +\tau {\vec {B}}}$

${\displaystyle {d{\vec {B}} \over ds}=\ \qquad \quad -\tau {\vec {N}}}$

onde ${\textstyle \kappa }$ é a curvatura e ${\textstyle \tau }$ é a torção.

As fórmulas Frenet–Serret são também conhecidas como teoremas de Frenet–Serret, e podem ser apresentadas de forma mais concisa usando a notação matricial:

${\displaystyle \left[{\begin{matrix}{\vec {T}}'\\{\vec {N}}'\\{\vec {B}}'\end{matrix}}\right]=\left[{\begin{matrix}0&\kappa &0\\-\kappa &0&\tau \\0&-\tau &0\end{matrix}}\right]\left[{\begin{matrix}{\vec {T}}\\{\vec {N}}\\{\vec {B}}\end{matrix}}\right]}$

Essa matriz é antissimétrica.

Prova

Considere a matriz:

${\displaystyle Q=\left[{\begin{matrix}\mathbf {T} \\\mathbf {N} \\\mathbf {B} \end{matrix}}\right]}$

As linhas dessa matriz são vetores unitários mutualmente perpendiculares: uma base ortonormal ℝ³. Como resultado, a transposta de Q é igual a inversa de Q: Q é uma matriz ortogonal. É suficiente mostrar que:

${\displaystyle \left({\frac {dQ}{ds}}\right)Q^{T}=\left[{\begin{matrix}0&\kappa &0\\-\kappa &0&\tau \\0&-\tau &0\end{matrix}}\right]}$

Note que na primeira linha a equação já se sustenta pela definição da normal ${\displaystyle {\vec {N}}}$ e da curvatura ${\displaystyle \kappa }$. Então é suficiente mostrar que ${\displaystyle \left({\frac {dQ}{ds}}\right)Q^{T}}$ é uma matriz antissimétrica. Já que ${\displaystyle I=QQ^{T}}$, tomando a derivada e aplicando a regra do produto resulta em:

${\displaystyle {\begin{aligned}0={\frac {dI}{ds}}=\left({\frac {dQ}{ds}}\right)Q^{T}+Q\left({\frac {dQ}{ds}}\right)^{T}\implies \left({\frac {dQ}{ds}}\right)Q^{T}=-\left(\left({\frac {dQ}{ds}}\right)Q^{T}\right)^{T}\\\end{aligned}}}$

que estabelece a antissimetria necessária.^[5]

Curvatura

A curvatura ${\displaystyle \kappa }$ em um ponto de uma curva mede a velocidade em que o vetor tangente ${\displaystyle {\vec {T}}(t)\,}$varia em relação ao comprimento de arco s. Ou seja, a curvatura é uma função escalar de s, definida como:

${\displaystyle \kappa (s)={\frac {|dT|}{|ds|}}}$ (1)

Porém o parâmetro s não é muito prático. Transformamos, então, ${\displaystyle \kappa }$(s) em ${\displaystyle \kappa }$(t), onde o parâmetro t pode ser um ângulo ou a variável tempo.

Usando a regra da cadeia:

${\displaystyle {\frac {|dT|}{|ds|}}={\frac {\frac {d{\vec {T}}}{dt}}{\frac {ds}{dt}}}=}$ ${\displaystyle {\frac {\vec {T'(t)}}{\frac {ds}{dt}}}}$ (2)

e

${\displaystyle {\frac {ds}{dt}}={\sqrt {x'^{2}+y'^{2}}}={\sqrt {{\vec {r'}}.{\vec {r'}}}}=|{\vec {r'(t)}}|}$ (3)

Substituindo (3) em (2) e esta na definição (1), teremos:

${\displaystyle \kappa (t)={\frac {\vec {T'(t)}}{|{\vec {r'(t)}}|}}}$ , ${\displaystyle |{\vec {r'(t)}}|\neq 0}$

Raio de curvatura

O raio de curvatura ${\displaystyle \rho }$ está associada com a curvatura ${\displaystyle \kappa }$ e é definido como

${\displaystyle \rho (t)={\frac {1}{\kappa (t)}}}$

Podemos então concluir que quanto maior a curvatura ${\displaystyle \kappa }$(t) em um certo ponto, menor será seu raio de curvatura ${\displaystyle \rho (t)}$. Em geral, se uma curva no espaço bidimensional tem curvatura ${\displaystyle \kappa }$ no ponto P(x,y), então o círculo de raio ${\displaystyle \rho =1/\kappa }$ que seja tangente a essa curva em P e que tenha centro no lado côncavo da curva em P é chamado de círculo de curvatura ou círculo osculador em P.

O círculo osculador e a curva não só se tocam em P como também têm a mesma curvatura naquele ponto. Dessa maneira, o círculo osculador é o círculo que melhor aproxima a curva na vizinhança de P. Por sua vez, o raio ${\displaystyle \rho }$ de um círculo osculador em P é chamado de raio de curvatura em P e o centro do círculo é chamado de centro de curvatura em P^[6].

O centro do círculo osculador é dado pela equação ${\displaystyle {\vec {O}}={\vec {P}}+\rho {\vec {N}}}$.

Aceleração expressa em termos dos vetores ${\displaystyle {\vec {T}}}$ e ${\displaystyle {\vec {N}}}$^[3]

Sendo ${\displaystyle {\vec {r}}(t)}$ a curva da trajetória de uma partícula, onde ${\displaystyle t}$ representa o parâmetro tempo, definimos a velocidade da partícula como ${\displaystyle {\vec {v}}(t)={d{\vec {r}} \over dt}=v{\vec {T}}}$, sendo ${\displaystyle v=|{\vec {v}}(t)|}$.

Partindo da definição ${\displaystyle {\vec {a}}(t)={d{\vec {v}} \over dt}}$, obtemos ${\displaystyle {d(v{\vec {T}}) \over dt}={dv \over dt}{\vec {T}}+v{d{\vec {T}} \over dt}}$.

O primeiro termo ${\displaystyle {dv \over dt}}$é definido como a componente tangencial da aceleração ${\displaystyle a_{T}}$, que pode ser interpretado como a variação do módulo da velocidade da partícula.

Utilizando as equações ${\displaystyle {\vec {N}}(t)={\frac {{\vec {T}}(t)\,'}{|{\vec {T}}(t)\,'|}}}$, ${\displaystyle \kappa (t)={1 \over \rho }}$ e ${\displaystyle \kappa (t)={\frac {\vec {T'(t)}}{|{\vec {r'(t)}}|}}}$, podendo esta última ser escrita como ${\displaystyle \kappa (t)={\frac {|{\vec {T'(t)|}}}{v}}}$, reescrevemos o segundo termo ${\displaystyle v{d{\vec {T}} \over dt}}$ como ${\displaystyle v{\vec {T}}'(t)=v|{\vec {T}}|{\vec {N}}=\kappa v^{2}{\vec {N}}={v^{2} \over \rho }{\vec {N}}}$. Assim, definimos a componente normal da aceleração como ${\displaystyle a_{N}={\frac {v^{2}}{\rho }}}$. Essa componente do vetor aceleração pode ser interpretada como a variação da direção da velocidade da partícula.

Dessa forma, foi demonstrado que ${\displaystyle {\vec {a}}=a_{T}{\vec {T}}+a_{N}{\vec {N}}}$. Conclui-se que, mesmo para curvas em três dimensões, o vetor aceleração sempre estará contido no plano formado por ${\displaystyle {\vec {T}}}$ e ${\displaystyle {\vec {N}}}$.

Torção

A torção ${\displaystyle \tau }$ mede a capacidade de uma curva se torcer e é definida como:

${\displaystyle \tau (s)={\frac {|d{\vec {B}}|}{|ds|}}}$

E assim como na curvatura, transformamos ${\displaystyle \tau (s)}$ em ${\displaystyle \tau (t)}$, pois s não é um parâmetro muito prático.

Pela regra da cadeia:

${\displaystyle |\tau (t)|={\frac {\frac {|d{\vec {B}}|}{|dt|}}{\frac {|ds|}{|dt|}}}={\frac {|{\vec {B'(t)}}|}{|{\vec {r'(t)}}|}}}$

Raio de Torção

Pode-se atribuir ao conceito de torção ${\displaystyle \tau }$, a ideia de raio de torção,^[7] denotado por σ, definido da forma:

${\displaystyle \sigma (t)={\frac {1}{\tau (t)}}}$

Expansão de Taylor

Diferenciando repetidamente a curva e aplicando as fórmulas de Frenet-Serret resulta na seguinte aproximação de Taylor para a curva próximo de s=0.^[8]

${\displaystyle \mathbf {r} (s)=\mathbf {r} (0)+\left(s-{\frac {s^{3}\kappa ^{2}(0)}{6}}\right)\mathbf {T} (0)+\left({\frac {s^{2}\kappa (0)}{2}}+{\frac {s^{3}\kappa '(0)}{6}}\right)\mathbf {N} (0)+\left({\frac {s^{3}\kappa (0)\tau (0)}{6}}\right)\mathbf {B} (0)+o(s^{3}).}$

Para uma curva genérica com torsão não nula, a projeção da curva em vários planos coordenados no sistema de coordenadas T, N, B em s=0 tem as seguintes interpretações:

• O plano osculante é plano contendo T e N. A projeção da curva neste plano tem a forma:

${\displaystyle \mathbf {r} (0)+s\mathbf {T} (0)+{\frac {s^{2}\kappa (0)}{2}}\mathbf {N} (0)+o(s^{2}).}$

Isso é uma parábola a termos de (s²), cuja curvatura em 0 é igual a k(0).n

• O plano normal é o plano contendo B e N. A projeção da curva neste plano tem a forma:

${\displaystyle \mathbf {r} (0)+\left({\frac {s^{2}\kappa (0)}{2}}+{\frac {s^{3}\kappa '(0)}{6}}\right)\mathbf {N} (0)+\left({\frac {s^{3}\kappa (0)\tau (0)}{6}}\right)\mathbf {B} (0)+o(s^{3})}$

que é uma parábola semicúbica de ordem o(s³).

• O plano retificador é o plano contendo T e B. A projeção da curva nesse plano tem a forma:

${\displaystyle \mathbf {r} (0)+\left(s-{\frac {s^{3}\kappa ^{2}(0)}{6}}\right)\mathbf {T} (0)+\left({\frac {s^{3}\kappa (0)\tau (0)}{6}}\right)\mathbf {B} (0)+o(s^{3})}$

que traça o gráfico de um polinômio cúbico de ordem o(s³).

Casos Especiais

Caso a curvatura (k(t)) for igual a zero, então a curva será uma linha reta, e os vetores N e B não estarão definidos.

Caso a torção (𝜏(t)) for igual a zero, então a curva estará em um plano.

Hélices possuem curva e torção constantes, entretanto uma curva pode ter torção nula e curvatura não nula: é o caso de círculos, parábolas, e diversas outras formas bidimensionais. O contrário não ocorre para curvas regulares.

Referências

Este artigo sobre matemática é um esboço. Você pode ajudar a Wikipédia expandindo-o. v d e