Konvex burok

A matematikában az euklideszi sík vagy euklideszi tér (vagy általánosabban, egy valós számok fölötti affin tér) X ponthalmazának konvex burka vagy konvex burkolója az a legkisebb konvex halmaz, ami X-et tartalmazza. Ha X a sík korlátos halmaza, a konvex burok elképzelhető úgy is, mintha X köré gumiszalagot feszítenénk.^[1]

Formálisan a konvex burok definiálható úgy is, mint az X-et tartalmazó összes konvex halmaz metszete, vagy az X pontjai összes konvex kombinációjának halmaza. Ez utóbbi definíció segítségével a konvex burok definíciója kiterjeszthető az euklideszi terekről tetszőleges valós vektorterekre; ez pedig tovább általánosítható irányított matroidokra.^[2]

A síkban vagy más, alacsony dimenziójú euklideszi terekben elhelyezkedő véges ponthalmaz konvex burka előállításának algoritmikus problémája a számítási geometria alapvető problémáinak egyike.

Definíciók

Egy ponthalmaz definíció szerint akkor konvex, ha bármely két pontját összekötő egyenes szakasz pontjait is tartalmazza. Ekkor adott X halmaz konvex burka a következő módokon definiálható:

1. Az (egyedi) minimális, X-et tartalmazó konvex halmaz
2. Az X-et tartalmazó összes konvex halmaz metszete
3. Az X pontjai összes konvex kombinációinak halmaza
4. Az összes, X-ben található csúcsokkal rendelkező szimplex uniója.

Az első definícióról nem nyilvánvaló, hogy működhet: miért lenne biztos, hogy minden X-re létezik az X-et tartalmazó egyedi, minimális konvex halmaz? A második meghatározás, miszerint az X-et tartalmazó összes konvex halmaz metszete, már jól definiált, és minden más, X-et tartalmazó Y halmaz részhalmaza, hiszen X a metszésbe hozott halmazok között szerepel. Tehát éppen egyedi minimális konvex halmaz, ami X-et tartalmazza. Minden, X-et tartalmazó konvex halmaznak (a konvexitás miatt) tartalmaznia kell X pontjainak összes konvex kombinációját, tehát az összes konvex kombináció halmaza részhalmaza az összes X-et tartalmazó konvex halmaz metszetének. Megfordítva, az összes konvex kombináció halmaza önmaga is az X-et tartalmazó konvex halmaz, tehát szintén tartalmazza az összes X-et tartalmazó konvex halmaz metszetét, tehát a két definíció által meghatározott halmazok azonosak. Valójában, Caratheodory tétele szerint, ha X egy N dimenziós vektortér részhalmaza, a fenti definícióban mindössze N + 1 pont konvex kombinációjára van szükség. Tehát a síkban a három vagy több pont alkotta X halmaz konvex burka megegyezik az X ponthármasai által meghatározott összes háromszög uniójával, általánosabban pedig az N dimenziós térben a konvex burok megegyezik a legalább N + 1 pontból álló X pont-N-esei által meghatározott szimplexek uniójával.

Ha X konvex burka zárt halmaz (ami például akkor következik be, ha X véges halmaz, vagy általánosabban, egy kompakt halmaz), akkor az megegyezik az összes, X-et tartalmazó zárt féltér metszetével. A hipersík-szeparációs tétel szerint ebben az esetben a konvex burkon kívül eső bármely pont a konvex buroktól alkalmasan megválasztott féltérrel elválasztható. Léteznek azonban olyan konvex halmazok, illetve ezek burkai, melyek nem reprezentálhatók ilyen módon – például a nyílt félterek is ilyenek.

Elvontabban, a Conv() konvexburok-művelet a lezárási operátor jellemző tulajdonságaival rendelkezik:

• Extenzív, ami azt jelenti, hogy bármely X konvex burka az X bővebb halmaza.
• nem csökkenő, tehát bármely X és Y halmazra, ahol X ⊆ Y, az X konvex burka is részhalmaza Y konvex burkának.
• Idempotens, tehát bármely X halmaz konvex burka megegyezik az X halmaz konvex burkának konvex burkával.

Véges ponthalmaz konvex burka

Egy véges ${\displaystyle S}$ ponthalmaz konvex burka megegyezik pontjai lehetséges konvex kombinációinak halmazával. Egy konvex kombinációban minden ${\displaystyle S}$-beli ${\displaystyle x_{i}}$ ponthoz egy ${\displaystyle \alpha _{i}}$ súlyt vagy együtthatót rendelnek olyan módon, hogy a súlyok nem negatívak, összegük pedig éppen egy. A súlyok segítségével kiszámítható a pontok súlyozott átlaga. Bárhogyan választják meg az együtthatókat, a létrejött konvex kombináció a konvex burok egy pontját adja, a teljes konvex burok pedig létrejön, ha az összes lehetséges konvex kombináció megalkotásával. Egyetlen képletben kifejezve, a konvex burok a következő halmazzal egyezik meg:

${\displaystyle \mathrm {Conv} (S)=\left\{\left.\sum _{i=1}^{|S|}\alpha _{i}x_{i}\ \right|(\forall i:\alpha _{i}\geq 0)\wedge \sum _{i=1}^{|S|}\alpha _{i}=1\right\}.}$

Az ${\displaystyle S\subsetneq \mathbb {R} ^{n}}$ véges ponthalmaz konvex burka az n = 2 esetben konvex sokszög, általánosabban az ${\displaystyle \mathbb {R} ^{n}}$-t tekintve konvex politóp. Az ${\displaystyle S}$ minden ${\displaystyle x_{i}}$ pontja, ami nincs benne a többi pont konvex burkában (tehát: ${\displaystyle x_{i}\notin \operatorname {Conv} (S\setminus \{x_{i}\})}$) a ${\displaystyle \operatorname {Conv} (S)}$ egy csúcsa. Valóban, minden ${\displaystyle \mathbb {R} ^{n}}$-beli konvex politóp megegyezik a csúcsok konvex burkával.

Ha ${\displaystyle S}$ pontjai mind egy egyenesre esnek, a konvex burok a legszélső két pontot összekötő egyenes szakasszal egyezik meg. Ha az ${\displaystyle S}$ a sík nem üres, véges részhalmaza, képzeletben kifeszíthetünk egy gumiszalagot úgy, hogy körbevegye a teljes ${\displaystyle S}$-t, majd elengedjük, hogy összehúzódhasson; mikor feszes lesz, éppen az ${\displaystyle S}$ konvex burkát foglalja magába.^[1]

Két dimenzióban a konvex burkot néha két töröttvonalra bontják, a felső és az alsó burokra, melyek a burok legbaloldalibb, illetve legjobboldalibb pontjai között feszülnek. Általánosabban, tetszőleges dimenzióban elhelyezkedő általános helyzetű pontok esetében a konvex burok minden eggyel alacsonyabb dimenziós „lapja” vagy fölfelé (elválasztva a burkot a fölötte lévő pontoktól), vagy lefelé mutat; a fölfelé mutató lapok uniója egy topologikus korongot alkot, ami a felső burok; hasonlóan, a lefelé mutató lapok uniója alkotja az alsó burkot.^[3]

Konvex burok kiszámítása

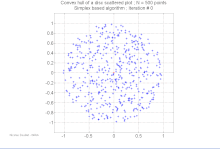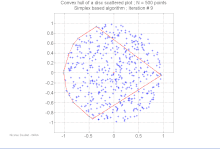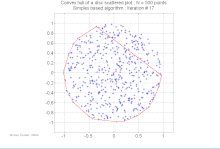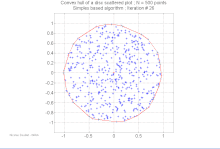
Bővebben: Konvex burok keresése

A számítási geometria területén több algoritmus ismert véges ponthalmazok és más mértani objektumok konvex burkának kiszámítására.

A konvex burok meghatározása a kívánt konvex alakot leíró egyértelmű, hatékony adatstruktúra előállítását jelenti. A megfelelő algoritmusok bonyolultságát általában a bemeneti pontok, n, illetve a konvex burok pontjai, h függvényében adják meg.

Két, illetve három dimenzióban több olyan kimenetérzékeny algoritmus ismert, ami a konvex burkot O(n log h) időben meghatározza. Háromnál magasabb d dimenziókban a konvex burok kiszámításához az eddig ismert algoritmusoknak ${\displaystyle O(n^{\lfloor d/2\rfloor })}$ időre van szükség, ami éppen a kimenetérzékeny algoritmus bonyolultsága a legrosszabb esetben.^[4]

Minkowski-összeg és konvex burkok

Bővebben: Minkowski-összeadás

Bővebben: Shapley–Folkman-lemma

A konvex burok képzésének művelete „jól viselkedik” a halmazok Minkowski-összeadását tekintve.

• Valós vektortérben a két (nem üres) ₁ és S₂ halmaz Minkowski-összege definíció szerint az S₁ + S₂, az összegzendők vektorainak elemenkénti összegzésével képezett összeg:

S₁ + S₂ = { x₁ + x₂ : x₁ ∈ S₁ és x₂ ∈ S₂ }.

Általánosabban, az S_n véges (nem üres) halmazcsalád Minkowski-összege definíció szerint az összegzendők vektorainak elemenkénti összegzésével képezett összeg:

∑ S_n = { ∑ x_n : x_n ∈ S_n }.

• Egy valós vektortér minden S₁ és S₂ részhalmazára igaz, hogy Minkowski-összegük konvex burka megegyezik konvex burkaik Minkowski-összegével:

Conv( S₁ + S₂ ) = Conv( S₁ ) + Conv( S₂ ).

Ez általánosabban bármennyi véges, nem üres halmazra is kimondható:

Conv(  ∑ S_n  ) = ∑ Conv( S_n ).

Más szavakkal, a Minkowski-összegzés és a konvex burok képzése kommutatív műveletek.^[5][6]

A fentiekből látszik, hogy a Minkowski-összeadás jelentősen különbözik a halmazelmélet unió műveletétől; és valóban, két konvex halmaz uniója nem feltétlenül konvex: általános esetben a Conv(S) ∪ Conv(T) ⊆ Conv(S ∪ T) valódi részhalmazt és nem egyenlőséget jelent. A konvex burok művelet kell ahhoz, hogy a konvex halmazok halmaza teljes hálót alkosson, melynek az unió (egyesítés) művelete a konvex halmazok uniójának konvex burkával egyezik meg:

Conv(S) ∨ Conv(T) = Conv( S ∪ T ) = Conv( Conv(S) ∪ Conv(T) ).

Más struktúrákkal való kapcsolata

Egy ponthalmaz Delaunay-háromszögelése és annak duálisa, a Voronoj-cella matematikailag a konvex burkok rokonainak tekinthetők: egy Rⁿ-beli ponthalmaz Delaunay-háromszögelése tekinthető úgy is, mint egy Rⁿ⁺¹-beli konvex burok projekciója.^[7]

Topologikusan tekintve, egy nyílt halmaz konvex burka mindig nyílt, egy kompakt halmazé pedig mindig kompakt; léteznek azonban olyan tárt halmazok, melyek konvex burka nem zárt.^[8] Például a

${\displaystyle \left\{(x,y)\mid y\geq {\frac {1}{1+x^{2}}}\right\}}$

zárt halmaz konvex burka a nyitott felső félsík.

Alkalmazásai

A konvex burok előállításának számos gyakorlati alkalmazása van az alakfelismerés, képfeldolgozás, a statisztika, földrajzi információs rendszerek, a játékelmélet, fázisdiagramok előállítása, az absztrakt interpretáció-alapú statikus kódanalízis területén. Eszközként, építőelemként is szolgál más számítási geometriai algoritmusok részeként, ilyen például a ponthalmaz szélességét és átmérőjét megállapító forgó tolómérce módszer.

A konvex burok fogalma az etológiában minimális konvex sokszög (MCP) néven ismert, ami egy állat mozgáskörzetének klasszikus, bár leegyszerűsítő megközelítése azon pontok alapján, ahol az állatot megfigyelték.^[9] A kiugró értékek az MCP-t rendkívül megnövelhetik, ezért szokás olyan megközelítést alkalmazni, hogy csak a megfigyelések egy részét veszik bele az MCP-be (például úgy, hogy az a pontok 95%-át tartalmazza).^[10]

Kapcsolódó szócikkek

• Affin burok
• Alfa-burok
• Choquet-elmélet
• Helly-tétel
• Holomorfan konvex burok
• Konkáv halmaz
• Konvex rétegek
• Krein–Milman-tétel
• Lineáris burok
• Maximális területű konvex sokszög
• Oloid
• Ortogonális konvex burok

Fordítás

• Ez a szócikk részben vagy egészben a Convex hull című angol Wikipédia-szócikk ezen változatának fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.

Jegyzetek

Források

• Andrew, A. M. (1979), "Another efficient algorithm for convex hulls in two dimensions", Information Processing Letters 9 (5): 216–219, DOI 10.1016/0020-0190(79)90072-3.
• Brown, K. Q. (1979), "Voronoi diagrams from convex hulls", Information Processing Letters 9 (5): 223–228, DOI 10.1016/0020-0190(79)90074-7.
• de Berg, M.; van Kreveld, M. & Overmars, Mark et al. (2000), Computational Geometry: Algorithms and Applications, Springer, pp. 2–8, <https://books.google.com/books?hl=en&lr=&id=tkyG8W2163YC&oi=fnd&pg=PA2>.
• Chazelle, Bernard (1993), "An optimal convex hull algorithm in any fixed dimension", Discrete and Computational Geometry 10 (1): 377–409, doi:10.1007/BF02573985, <http://www.cs.princeton.edu/~chazelle/pubs/ConvexHullAlgorithm.pdf>.
• Grünbaum, Branko (2003), Convex Polytopes (2nd ed.), Graduate Texts in Mathematics, Springer, ISBN 9780387004242.
• Kernohan, Brian J.; Gitzen, Robert A. & Millspaugh, Joshua J. (2001), Joshua Millspaugh, John M. Marzluff, ed., Ch. 5: Analysis of Animal Space Use and Movements, Academic Press, ISBN 9780080540221.
• Knuth, Donald E. (1992), Axioms and hulls, vol. 606, Lecture Notes in Computer Science, Heidelberg: Springer-Verlag, p. ix+109, ISBN 3-540-55611-7, doi:10.1007/3-540-55611-7, <http://www-cs-faculty.stanford.edu/~uno/aah.html> Archiválva 2017. június 20-i dátummal a Wayback Machine-ben.
• Krein, M. & Šmulian, V. (1940), "On regularly convex sets in the space conjugate to a Banach space", Annals of Mathematics, 2nd ser. 41: 556–583, DOI 10.2307/1968735.
• Schneider, Rolf (1993), Convex bodies: The Brunn–Minkowski theory, vol. 44, Encyclopedia of Mathematics and its Applications, Cambridge: Cambridge University Press, ISBN 0-521-35220-7.

További információk

• Weisstein, Eric W.: Convex Hull (angol nyelven). Wolfram MathWorld
• "Convex Hull" by Eric W. Weisstein, Wolfram Demonstrations Project, 2007.